Building Mathematical Foundations for Educational Information (Excerpt from Knowing the Learner)
Thank you for visiting the Mathematical Foundations blog. You are welcome to view the blog post and the comments.
The following passage is excerpted from chapter VII of Knowing the Learner. It suggests productive directions to be taken in working with strictly educational information, i.e. practical learning outcomes. These directions are designed to maximize the educational usefulness to teachers, and indeed the full range of educational stakeholders, of such information.
Building Mathematical Foundations
for Educational Information
Educational activities can be defined operationally as efforts to realize valued learning outcomes. The central information challenge in support of such efforts is producing actionable data in real-time instructional settings (i.e., information on how well targeted learning outcomes have been attained). The conceptual foundation for producing this information is the practical learning goal – that is, the statement of intended learning outcomes at a level of specificity appropriate for instruction. The most central educational research questions – e.g., the search for effects of methods of instruction – must rely on such information as the basis for their inferences.
Of particular value is information on how well core capabilities have been attained, as these hold the possibility of heightening and multiplying effects of learning. If we do not limit ourselves to outcome information on knowledge and skills but also consider information on dispositions, then we can begin to build the increasingly complete picture of the learner that is needed for emerging educational purposes.
Consider the case of proportional reasoning, a skill that may be considered a core capability in that it is prerequisite to competent participation in math, science, and technology in schoolwork, and to adequately grasping many contemporary economic and social issues.
The concept of proportionality is essential to understanding much in science, mathematics and technology. Many familiar variables such as speed, density and map scales are ratios or (rates) themselves.
(American Association for the Advancement of Science (AAAS), 2001, p. 118)
Consider one aspect of proportional reasoning in particular – the ability to effectively coordinate two ratios to solve a problem. In the following case drawn from the Cubes and Liquids assessment activity, proportional reasoning plays a role in predicting whether a solid object will float in a liquid. A successful prediction involves the coordination of the density of the solid object and the density of the liquid into which it is to be immersed. Densities of the objects and the liquids are each conceptualized as the ratios of their respective masses and volumes. The nature of the problem then is such that these two ratios need to be coordinated. Figure 7.1 displays the results of an assessment based on this assessment activity.
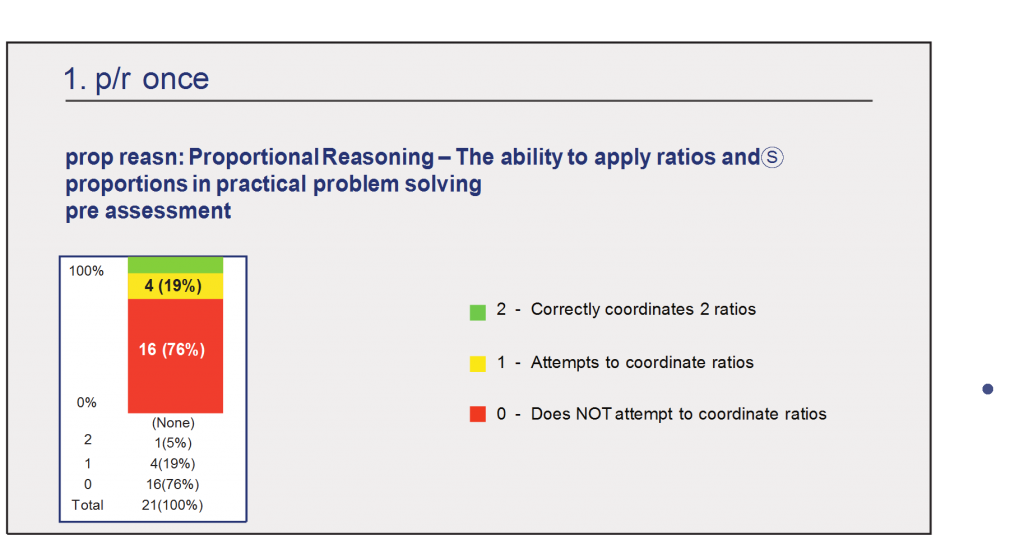
The high percentage of students who show no evidence of attainment of this capability indicates a need for instruction. In planning instruction for this group, the teacher will be interested in knowing how well individual students have attained the capability and how well the class as a whole performed on the task. This information
is displayed in Figure 7.2.
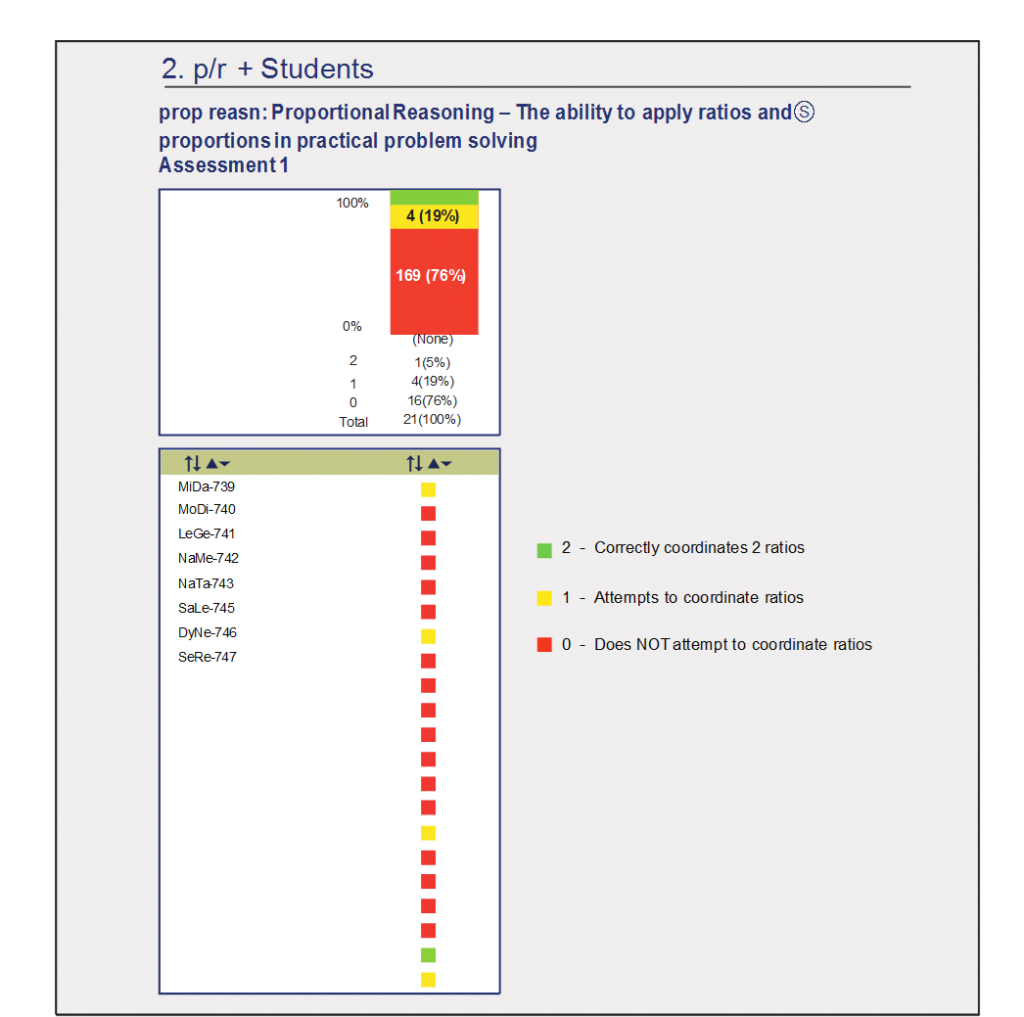
Having any information at all on student attainment of targeted learning goals can provide invaluable input for planning the next steps in instruction. As our long- time colleague and fellow ACASE founder, Tom Hick, has been known to say: “The data you have is the best data you have.” But this leads inevitably and rightly to the question: How can this data be improved? One improvement would be to obtain an indication of how confident we can be in the assessment results. Multiple assessments of attainment of a learning goal can serve that purpose. As instruction progresses and additional assessments are conducted, the picture fills out, as in Figure 7.3.
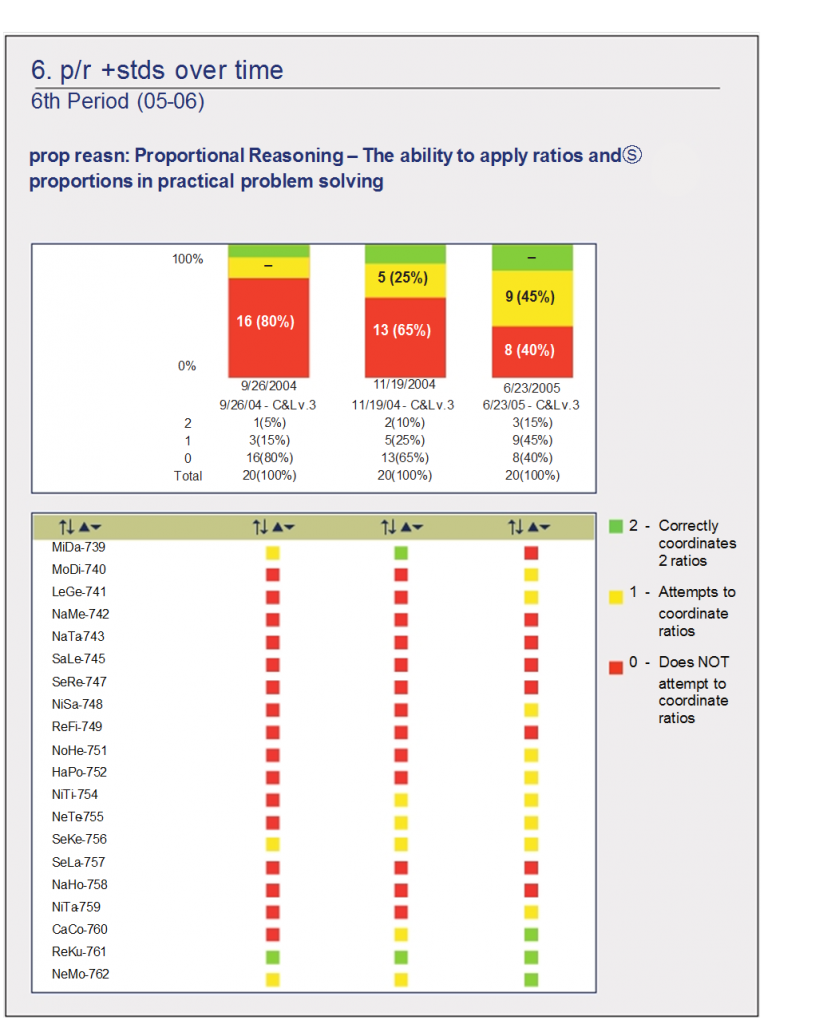
The strength of our confidence in the individual ratings builds from additional assessment information as instruction proceeds. For those students who are rated at the same level of attainment on three occasions, we can be pleased with the reliability of our ratings, though not necessarily with the resulting attainment. A progression of ratings in the direction of red to yellow to green over time is also consistent with desired properties of the assessment instrument and so overall evidence begins to accumulate concerning reliability and validity of the assessment instrument. These all provide increasingly stronger indications for what is needed next in instruction.
The rating for the first student, MiDa, appears problematic. Did MiDa have a “bad day” in June? Did the teacher make an error in scoring the assessment results? Is there a flaw in the assessment instrument or process? Has instruction been inappropriate for this student in some way? Such a result calls for evaluation of one or more features of the educational activities underway.
As long as competence in proportional reasoning remains a targeted learning goal, such reports can continue to follow students through their careers, providing the critical information needed to plan, evaluate, and improve instruction. Imagine next year’s science or mathematics teacher having this assessment information available as a basis for planning instruction for these same students. But can this information be improved further? Three questions can lead the way to consideration of how to improve educational information:
- What level of attainment should be inferred for a student when results of multiple assessments are available? (For example, should the most recent level of attainment be preferred or is there another basis for making this inference?)
- How can confidence in the judgment of attainment of a learning goal be enhanced?
- How does the level of attainment on a given learning goal relate to the attainment of other learning goals and to the larger picture of the student’s participation in the instructional environment?
To approach these, we would like to bring to the attention of all of our readers (not just educational specialists) a family of probabilistic analysis techniques known as Bayesian statistics (McGrayne, 2011; Phillips, 1973). These methods are geared to persistently refresh estimates of likelihood based on incoming data from many possible sources. A Bayesian analysis is able take the results of the three assessments of proportional reasoning shown and, based on some heuristic rule that we have devised, to assign a current level of probability of attainment to each of the three levels for every student.
For example, imagine characterizing some aspect of proportional reasoning as having three levels of attainment:
Level 2 – Attained
Level 1 – Progressing
Level 0 – No evidence of attainment
At which level is the student most likely functioning? The history of a student’s attainment of these levels helps to draw a conclusion concerning the current level of attainment. But additional inputs drawn from a wider bank of information may also be helpful.
For example, the teacher may be privy to additional information concerning students’ capabilities beyond this particular set of assessments. The teacher is likely to have additional information that supports or contradicts the results of an assessment and would wish that additional information to be taken into consideration. Bayesian methods welcome human judgment as supplement to other sources of data and can give weight to such judgments in a way that will best incorporate them into the overall picture of student attainment.
More specifically, a combined pool of information can be drawn on to estimate the probabilities that a student is functioning at each of these three levels. Probabilities are typically construed as ranging from 0.0 (representing certainty of non-occurrence) to 1.0 (representing certainty of occurrence). For our student A, the estimate of the probability of “attained” may be 0.23; the probability of being at the level “progressing” 0.74; and the probability “no evidence of attainment” is the best judgment is 0.03. The only constraint on these values is that the probabilities must add up to 1.0, i.e., be mutually exclusive and exhaustive for each student on a single learning goal. Each time additional information arrives concerning this learning goal, the analysis and its estimates of probability can be refreshed.
There are actually many additional sources of information that can be helpful in making a judgment as to level of attainment of a capability. The educational program may lodge more data on students’ competence related to ratios (i.e., performing mathematical operations on fractions, percent, etc.). Or it may be that students who studied with a particular seventh-grade mathematics teacher tend to be particularly strong in working with ratios and proportions. Here is a place where the enormous banks of information concerning students that are lodged in schools may become of practical value – attendance, interests, dispositions, grades given by different teachers, performance on various tests and survey instruments, all could be incorporated via a Bayesian analysis to enrich the estimate of probability that a student is performing at some level of attainment of a capability. By incorporating such information from performance on other learning goals and other relevant features of the instructional environment, stronger and stronger estimates can be obtained to help the teacher know how likely it is that a student is performing at a particular level of attainment. This is with essentially no additional effort on the part of the teacher beyond calling up the most recent assessment results for any given learning goal. Sound human insight and judgment, which should always be at the heart of decision-making, can now enjoy a lively interaction with complex sources of information through data analytic processes devoted to estimating with increasing precision how well targeted learning goals have been attained by individuals and groups.
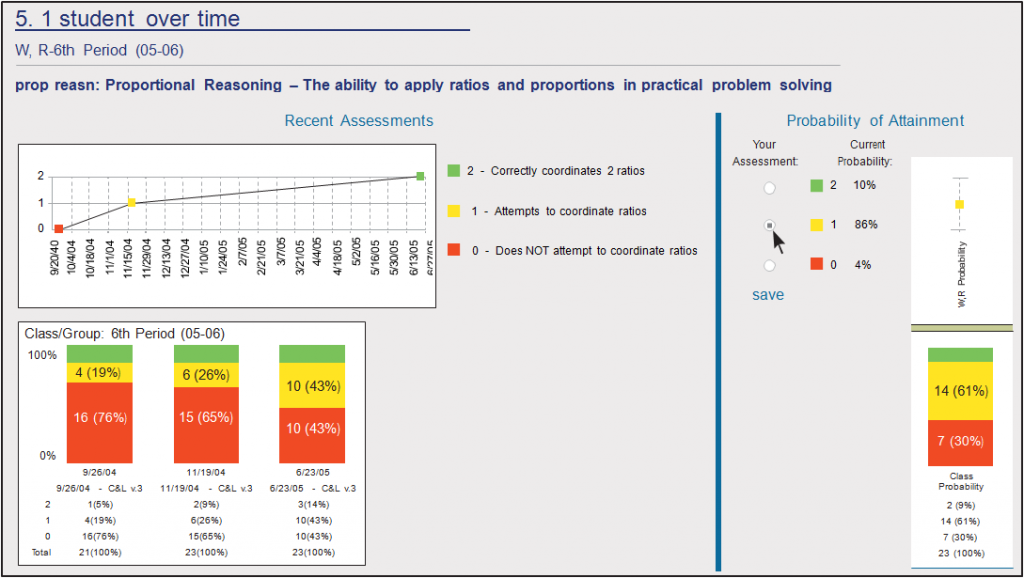
Figure 7.4 shows how this information would be displayed to help a teacher plan the next step of instruction related to proportional reasoning for student W,R and the class as a whole.
The left hand portion of Figure 7.4 displays assessment results on attainment of proportional reasoning for a class and for student W,R on three different occasions. On the basis of these three assessments alone, one might judge that the student has attained the top level of performance on this learning goal. However, the Current Probability levels on the right hand side of the graph, calculated from a computerized algorithm that incorporates additional sources of information, suggests that this may not be the case. Moreover, the Your Assessment buttons, which are the teacher’s means for incorporating an independent judgment into the analysis, shows that the teacher is about to enter and save a rating that differs from the rating based on the July 23 assessment results. Apparently, she is privy to information that contradicts the most recent assessment results. When she enters and saves her rating the Current Probability will likely strengthen the algorithm-based results. But actually there may be no need for her to intervene with a rating expressing her personal judgment, as the arrow in Figure 7.4 shows she is about to do. The computational algorithm that generates probabilities for the levels of attainment already has come to the same conclusion that she has – that the likelihood is quite low that the student is actually functioning at the level indicated by the July assessment results. But why should the student have been given an incorrect rating? Was it a slip of a rater’s finger? A fault in the assessment rubric? Is the same happening with other students as well? The teacher has indications here that suggest the need to reconsider the validity and reliability of the measures used. But there is another possibility. What if there is persistent disagreement between the teacher and the probability algorithm concerning the best estimate of student level of attainment? Perhaps the algorithm itself needs to be revised or refreshed.
This may seem an inordinate amount of attention given to a single capability, but it actually is precisely the necessary step forward. We must identify core capabilities, set aligned learning goals, build valid ways to assess their attainment, and have an indication of our confidence in assessment results to compose a useful picture of the degree to which learners have attained intended learning outcomes. Further, we must study the relationships between these capabilities. How do they inter-depend? What effect might the attainment of one learning outcome have on the attainment of others? This is precisely the type of information that is currently missing in attempts to answer simple questions such as – which methods of instruction and which program characteristics are most effective in facilitating attainment? The Student to the State sequence presented earlier shows how this very information can support policy planning and decision-making up and down educational institution hierarchies. Perhaps more importantly, each such piece of information increases our depth of knowing and understanding the learner.
Information on the relationship between practical learning outcomes is the needed direction to be taken for enriching educational research, as well as for supporting decision-making and action at the scene of educational events. Such relationships, possibly hierarchical and causal, could be a foundation for establishing an empirical basis for what we have been called learning progressions (Heritage, 2008; Schneider & Plasman, 2011) and also could serve as the basis for operationalizing Mauritz Johnson’s notion of a goal contribution unit ( Johnson, 1985).
Information technology now permits not only the analysis of immense quantities of information of this kind, but also extensive data entry options. A teacher can enter assessment ratings onto a mobile application while instruction is underway. Students can perform tasks and respond to questions on computers, clickers, and other mobile devices. The teacher (and students) can obtain near-real-time estimates of student attainment of targeted learning goals. Consider the full history of information that is regularly collected and stored regarding any particular student in existing school systems. Once coordinated with results concerning practical learning goals and outcomes, vast pools of information can be made productive at many levels of decision-making. Bayesian methods can turn big data into data that is the just right size for practical decision-making. Those interested in collaborating in this project will find resources and colleagues at the Forum for Educational Arts and Sciences (http://educationalrenewal.org/fellows/).
In the larger picture, such mathematical models and data analytics must always be the servants of purely educational purposes; institutional needs must not take priority over purely educational considerations. Nor, as John Tukey warns (Tukey, 1969), do we wish to bow to theories and methods that were developed for other purposes, particularly, in the case of the field of education, the norm-referenced testing paradigm that was developed for non-educational psychometric purposes. Moreover, please consider again the caveat that has accompanied all of our presentations in Knowing the Learner: Information on how well learning goals have been attained should not be used for non-educational purposes. When this point of view is adopted, it also becomes clear that it is not the internal features of tests – e.g., test items and right and wrong answers – that need to be kept secure, but rather information concerning individual students, so that it will not be misused. Generally speaking, we can conclude that information on student attainment is likely to be misused if it is being put to non-educational purposes. In attempting to understand the nature and actions of others, it is critical to never lapse into making another human being, teacher or student, simply an object of observation. We must exercise the same reverence for the other, the same respect for freedom and personal privilege that we would wish extended to ourselves.